Mūsā al-Khwārizmī
(A.D. 780 – 850)
Abū ʿAbdallāh Muḥammad ibn Mūsā al-Khwārizmī (Persian: عبدالله محمد بن موسى الخوارزمی), earlier transliterated as Algoritmi or Algaurizin, was a Persian mathematician, astronomer and geographer during the Abbasid Caliphate, a scholar in the House of Wisdom in Baghdad.
In the twelfth century, Latin translations of his work on the Indian numerals introduced the decimal positional number system to the Western world. His Compendious Book on Calculation by Completion and Balancing presented the first systematic solution of linear and quadratic equations in Arabic. In Renaissance Europe, he was considered the original inventor of algebra, although it is now known that his work is based on older Indian or Greek sources. He revised Ptolemy's Geography and wrote on astronomy and astrology.

A page from al-Khwārizmī's Algebra

House of Wisdom
The House of Wisdom (Arabic: بيت الحكمة; Bayt al-Hikma) was a major intellectual center during the Islamic Golden Age. The House of Wisdom was founded by Caliph Harun al-Rashid (reigned 786–809) and culminated under his son al-Ma'mun (reigned 813–833) who is credited with its formal institution. Al-Ma'mun is also credited with bringing many well-known scholars to share information, ideas, and culture in the House of Wisdom. Based in Baghdad from the 9th to 13th centuries, many learned scholars including those of Persian or Christian background were part of this research and educational institute. Besides translating books into Arabic and preserving them, scholars associated with the House of Wisdom also made many remarkable original contributions to diverse fields.
Al-Khwarizmi was a scholar and a founder of the House of Wisdom.He contributed to for the development of ideas. And he has opportunity to work with senior scholars.

Scholars at an Abbasid library. Maqamat of al-Hariri Illustration by Yahyá al-Wasiti, Baghdad 1237
Algebra
Al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala (Arabic: الكتاب المختصر في حساب الجبر والمقابلة, 'The Compendious Book on Calculation by Completion and Balancing') is a mathematical book written approximately 830 CE. The book was written with the encouragement of the Caliph al-Ma'mun as a popular work on calculation and is replete with examples and applications to a wide range of problems in trade, surveying and legal inheritance. The term algebra is derived from the name of one of the basic operations with equations (al-jabr, meaning "restoration", referring to adding a number to both sides of the equation to consolidate or cancel terms) described in this book. The book was translated in Latin as Liber algebrae et almucabala by Robert of Chester (Segovia, 1145) hence "algebra", and also by Gerard of Cremona. A unique Arabic copy is kept at Oxford and was translated in 1831 by F. Rosen. A Latin translation is kept in Cambridge.
It provided an exhaustive account of solving polynomial equations up to the second degree, and discussed the fundamental methods of "reduction" and "balancing", referring to the transposition of terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation.
Al-Khwārizmī's method of solving linear and quadratic equations worked by first reducing the equation to one of six standard forms (where b and c are positive integers)
-
squares equal roots (ax2 = bx)
-
squares equal number (ax2 = c)
-
roots equal number (bx = c)
-
squares and roots equal number (ax2 + bx = c)
-
squares and number equal roots (ax2 + c = bx)
-
roots and number equal squares (bx + c = ax2)
by dividing out the coefficient of the square and using the two operations al-jabr (Arabic: الجبر "restoring" or "completion") and al-muqābala ("balancing"). Al-jabr is the process of removing negative units, roots and squares from the equation by adding the same quantity to each side. For example, x2 = 40x − 4x2 is reduced to 5x2 = 40x. Al-muqābala is the process of bringing quantities of the same type to the same side of the equation. For example, x2 + 14 = x + 5 is reduced to x2 + 9 = x.
The above discussion uses modern mathematical notation for the types of problems which the book discusses. However, in al-Khwārizmī's day, most of this notation had not yet been invented, so he had to use ordinary text to present problems and their solutions. For example, for one problem he writes, (from an 1831 translation)
If some one say: "You divide ten into two parts: multiply the one by itself; it will be equal to the other taken eighty-one times." Computation: You say, ten less thing, multiplied by itself, is a hundred plus a square less twenty things, and this is equal to eighty-one things. Separate the twenty things from a hundred and a square, and add them to eighty-one. It will then be a hundred plus a square, which is equal to a hundred and one roots. Halve the roots; the moiety is fifty and a half. Multiply this by itself, it is two thousand five hundred and fifty and a quarter. Subtract from this one hundred; the remainder is two thousand four hundred and fifty and a quarter. Extract the root from this; it is forty-nine and a half. Subtract this from the moiety of the roots, which is fifty and a half. There remains one, and this is one of the two parts.
J. J. O'Conner and E. F. Robertson wrote in the MacTutor History of Mathematics archive:
Perhaps one of the most significant advances made by Arabic mathematics began at this time with the work of al-Khwarizmi, namely the beginnings of algebra. It is important to understand just how significant this new idea was. It was a revolutionary move away from the Greek concept of mathematics which was essentially geometry. Algebra was a unifying theory which allowed rational numbers, irrational numbers, geometrical magnitudes, etc., to all be treated as "algebraic objects". It gave mathematics a whole new development path so much broader in concept to that which had existed before, and provided a vehicle for future development of the subject. Another important aspect of the introduction of algebraic ideas was that it allowed mathematics to be applied to itself in a way which had not happened before.


His mind-expanding invention is:
Algebra(Al-Jabr)
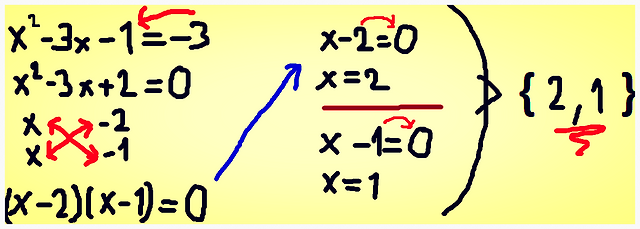
Gallery
To see details please click the images
 Corono Brezina's Book |  Khwarizmi's Statue |  Al-Khwarizmi's Planisphere |  Dixit algorizmi |  A translation |
|---|